Just because you can model the relationship between latent variables that are measured by multiple indicators doesn’t mean that you must. You can also model relationships between observed variables, just like path analysis. Let us say that you are researching SAT scores, and want to examine the relationship between education, income, and SAT scores. Figure 42 below specifies such as relationship.
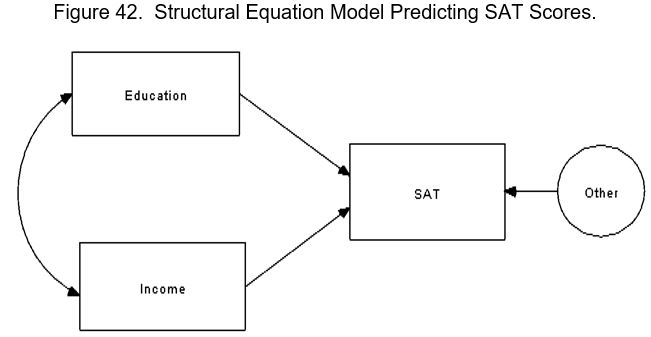
Note that the model indicates that education and income cause SAT scores; we know this because of the single-headed arrows pointing from the independent variables to the dependent variable. The curved arrow indicates that education and income will be correlated (because wealthier individuals tend to get more education). The “Other” represented by the circle is an error term; it is a circle because it was not observed, but rather it was estimated. This model would be more informative than an equivalent regression model because the error term is implicitly modeled rather than making the untenable assumption that it does not exist. Other than the minor “improvements” SEMs make, you can think of models like that as being identical to regression or path analysis.
“I strongly recommend that students try to set up any research problem under study in a path diagram. It forces one to conceptualize and bring out the basic structures of problems.”
-Fred Kerlinger
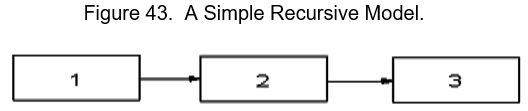
The “one-way” arrows represent Structural Regression Coefficients and indicate the impact (effect) of one variable on another. As we discussed above, SEMs can model “causal loops.” Models without such loops are said to be recursive.
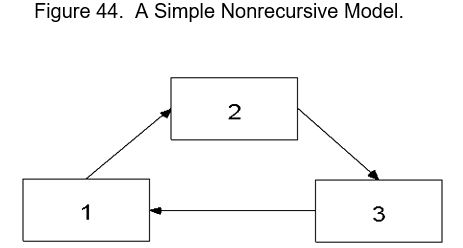
Models that do specify causal loops are said to be Nonrecursive; Causal flow (arrows) go both ways, such as in causal loops or reciprocal causation.
Last Modified: 02/14/2019
